Gas Laws

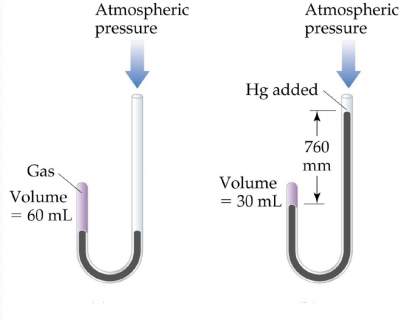
Boyle's Law

"Volume of a fixed quantity of gas is inversely proportional to its pressure"

V = constant × 1/P

PV = constant

Charles' Law

"The volume of a fixed quantity of gas at constant pressure increases as the temperature Increases"

V = constant × T

V / T = constant

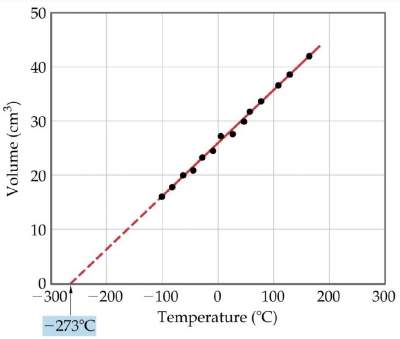Note:
When temperature is measured in °C, the intercept on the temperature axis is − 273.15°C (called absolute zero)

Avogadro's Law

"The volume of a gas at a given temperature and pressure is directly proportional to the number of moles of the gas"
V = constant × n
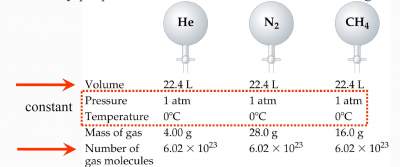
avogadro

Based on the three laws, we obtain V = constant × nT/P

Hence the Ideal Gas Law, V = R × nT/P →
Ideal Gas Law
PV = nRT

Where R is gas constant and its value depends on the units of P, V, T used.

STP (Standard Temperature & Pressure)are: T: 0°C; 273.15 K, P: 1 atm.
Volume of 1 mol of gas at STP is:
V = nRT/P = (1 mol)(0.08206 L·/mol·K)(273.15K)/ 1.000 atm = 22.4 L

For an ideal gas under 2 sets of conditions:
P₁V₁ = n₁RT₁ & P₂V₂ = n₂RT₂
Hence, R = P₁V₁ / n₁T₁ & R = P₂V₂ / n₂T₂
→ P₁V₁ / n₁T₁ = P₂V₂ / n₂T₂

Rearranging the gas law yields: n/V = P/RT
Multiply by the molar mass (M): nM/V = PM/RT
Since nM = w in grams)
(Gas density) d = PM/RT → (Molar Mass) M = dRT/P

Gas mixtures and partial pressures

"In a gas mixture the total pressure is given by the sum of partial pressures of each component"

Hence, P_total = P₁ + P₂ + P₁ + ....

Dalton's Law

Remark: If each gas obeys the ideal gas equation:
P_i = n(RT/V) where P_i is called Partial Pressure.
→ P_total = (n₁ + n₂ + n₃ + ....)(RT/V)

If n_i is the number of moles of gas (i) exerting a partial pressure
P_i = X_i P_total
where X_i (mole fraction) = n_i/n_total

Exercises on Gas Laws

Exercise I on Finding Total Pressure

Check your answers here: Solution to the Exercise I on Finding Total Pressure

Exercise II on Finding Total Pressure

Check your answers here: Solution to the Exercise II on Finding Total Pressure

Exercise III on Finding Total Pressure

Check your answers here: Solution to the Exercise III on Finding Total Pressure

For more details, please contact me here.
Date of last modification: 2024