Vector and Scalar Quantities, Vector Addition, and Vector Components
Vector and Scalar Quantities
Scalar
A scalar quantity is specified completely by its magnitude, that's a number and a unit.
Examples are speed (75 km/h, 55 mph), Distance (50 km, 10 feet), Volume (500 cm3, 45 feet3).
Scalar quantities that are measured in the same units may be added or subtracted in the usual way.
For example:
23mm + 7mm = 30 mm
54 m2 − 5 m2 = 49 m2
Vector
A vector quantity is specified completely by a magnitude and a direction.
It consists of a number, a unit, and a direction.
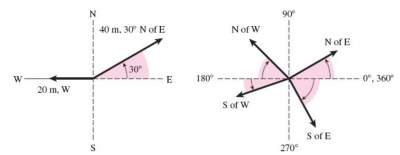
Examples are displacement (35 m, North) and velocity (70 km/h, 30° North of East).
The direction must be a part of any calculations involving vector quantity.
See example below in which the figure shows the direction of a vector by reference to North (N), South (S), East (E), and West (W).
Vectors are different from scalars:
- Vectors must be represented by: a magnitude + direction + units.
Scalars can be represented by: magnitude + units.
- Vectors can be added or subtracted using special methods.
Scalars can be added or subtracted simply using arithmetics operations.
Exercise with Solution: Vector or Scalar
Specify which one is vector or scalar:
| 15 m |
_________________ |
| 55 m/s, North |
_________________ |
| 15 km, South |
_________________ |
| 25 degrees Celsius |
_________________ |
| 10 exabytes |
_________________ |
| 100 calories |
_________________ |
Check your answers here:
Specify which one is vector or scalar
Learning Further details on Density of Regular and Irregular Shaped Objects is available through the link.
For more details, please contact me here.
