Speed and Velocity
Introduction
Just as distance and displacement have distinctly different meanings, so do speed and velocity.
Speed is a scalar quantity that refers to "how fast an object is moving."
Speed can be thought of as the rate at which an object covers distance and its formula is: v = d/t where d is the distance and t is time.
Example: Assume that Mike took him 2 hours minutes to walk 6 miles. What is his speed in miles per hour (mph) during this exercise?
Answer: v = 6 / 2 = 3 mph.
Exercise: Unit Conversion
Exercise 1:
Question: Convert 80 kilometers per hour to miles per hour.
Solution:
1 km = 0.6214 miles; 1 mile = 1.609 km
80 km/h × 0.6214 = 49.71 mph
Average Speed
Average Speed = Distance Traveled / Time of Travel
Exercise 2:
Question: Calculate the average speed of a Taxi driver who started a trip from point A to D passing by B and C with speed mentioned in the figure below:
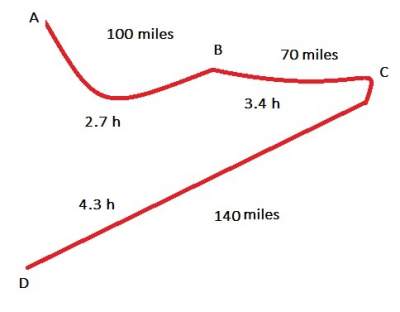
Check your answers here:
Solution: Average speed exercise
Question: Convert your answer to km/h.
Answer: 47.94 kmh,
Exercise
Adam drove for 4 hours at a rate of 70 miles per hour and for 3 hours at 55 miles per hour.
Question: What was his average speed for the entire trip?
Check your answers here:
Solution: Average Speed Exercise
Velocity
Velocity is a vector quantity that refers to "the rate at which an object changes its position."
As depicted below the velocity requires direction:
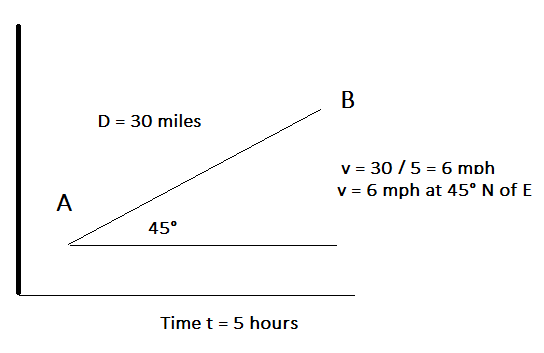
Average Velocity
Average Velocity = Displacement / Time = ΔPosition / Δt = Δd / Δt
Note the difference between distance and displacement.
- Displacement is "how far out of place an object is" it is the object's overall change in position.
- The speed at any instant is called instantaneous speed.
- The speedometer in the car gives instantaneous speed.
Exercise
Let's assume that Joe while jogging, during the first two hours of his exercise,
he ran a distance from work started from 0 to 8 miles, while the time in hours went from 0 to 2.
Question 1: Calculate his average velocity.
Question 2:
During the next three hours, the distance from his work went from 8 to 23 while the time went from 1 to 4.
Calculate his average velocity.
Check both answers here: Average Velocity Exercise
For more details, please contact me here.
Date of last modification: 2024

