Introduction to Work
Definition
Work: whenever a force acts through a distance, work is done in a way that can be measured or predicted.
Work is defined as the product of force and the distance through which the force moves an object in its direction.
Work depends on two elements: force and distance. For a constant force and a straight line motion, work is expressed as:
work = w = F×d
Work is a scalar quantity (magnitude with no direction) and is measured in joules (J).
1 joule = (1 newton) × (1 meter) = 1 N • m
For example, when a ball is thrown by the baseball players (pitchers),
the work done on the ball as it falls is equal to the weight of the ball (force) times the distance.

Basically, even if a considerable force F is exerted but distance is zero then the work accomplished is zero!
Impulse
The impulse is found using the Newton's second law F = m×a = m × Δv /t and if both sides are multiplied by t we obtain F ×t = m × Δv
We obtain the impulse and its unit is N•s.
Examples
Example 1
When lifting a box there is work being done but carrying it in the physics sense. Why?
Answer: When you a list a box, there was actually a force F exerted on the box and a distance from the ground until a body position.
However, carrying the box only without a movement then the work = 0.
Example 2
When you kick a ball, you do work on the ball (see picture below):

- The player foot exerts a force on the ball
- The player exert that force through kicking the ball
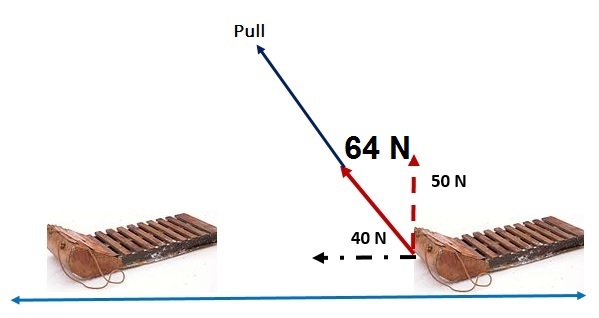
Impact of Parallel Forces on Work
- Only forces parallel to the motion do work.
- As per the figure below, with the block sliding horizontally, only the 40N part of the diagonal force does work.
Exercise
Exercise on Work
Check your answers here:
Solution to the Work Exercise
For more details, please contact me here.
Date of last modification: 2024


