The Variety of Demand Curves

Introduction

• The price elasticity of demand is related to the slope of the demand curve.
• Rule of thumb:
  The flatter the curve, the bigger the elasticity.
  The steeper the curve, the smaller the elasticity.
• Five different classifications of D curves.

Perfectly Inelastic Demand

Price of elasticity

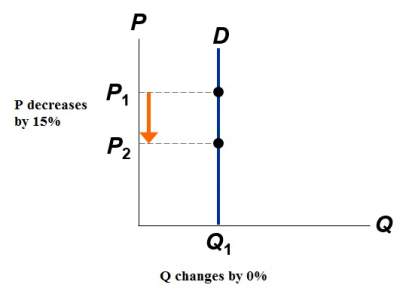
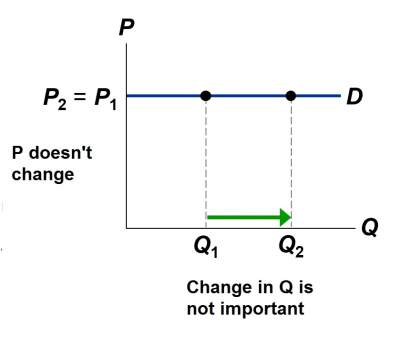
Elasticity D curve: Vertical Consumers' price sensitivity: None Elasticity: 0

Inelastic Demand

Inelastic Demand 1

Inelastic Demand-1 D curve: relatively steep Consumers' price sensitivity: relatively low Elasticity: < 1

Unit Elastic Demand

Unit Elastic

Unit Elastic 1 D curve: intermediate slope Consumers' price sensitivity: intermediate Elasticity: = 1

Elastic Demand

Elastic Demand 2

Elastic Demand-2 D curve: relatively flat Consumers' price sensitivity: relatively high Elasticity: > 1

Perfectly Elastic Demand

Perfectly Elastic

Perfectly Elastic-1 D curve: horizontal Consumers' price sensitivity: extreme Elasticity: ∞

Elasticity of a Linear Demand Curve

Price Elasticity and Total Revenue

• As illustrated in the previous example, where if price is increased from $250 to $350, and the question is: would your revenue rise or fall?
  The formula is: Revenue = P × Q
• A price increase has two effects on revenue:
  Higher price (P) means that we should expect increase in the revenue on each unit sold.
  However, whenever fewer units are sold leading to a decrease in quantity (Q), due to Law of Demand.
• Which of these two effects is more important?
  The answer is that it all depends on the price elasticity of demand.

• If demand is elastic, then price elasticity of demand > 1
• % change in Q > % change in P
• The fall in revenue from lower Q is greater than the increase in revenue from higher P, hence revenue falls.

Price Elasticity - Tot. Rev.

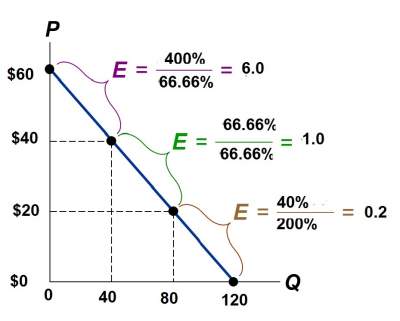
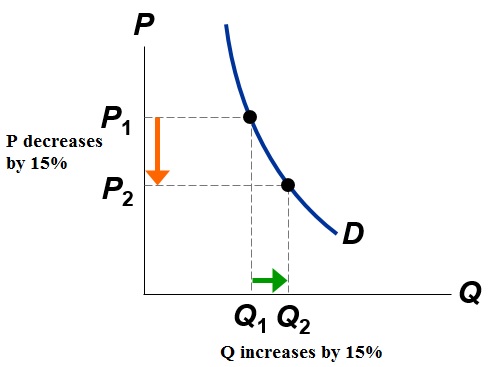
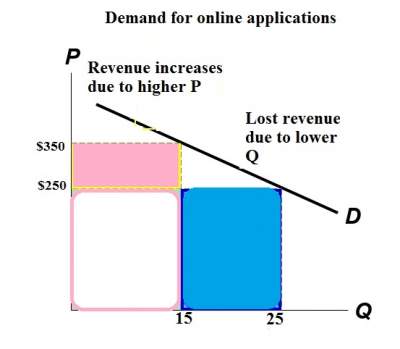
Elastic demand. In this case, elasticity = 1.5 If P = $250, Q = 25 and revenue = $6250 If P = $350, Q = 15 and revenue = $5250 When D is elastic, a price increase causes revenue to fall.

On the other hand,
• If demand is inelastic, then price elasticity of demand < 1
  Percentage of change in Q < Percentage of change in P
• The fall in revenue from lower Q is less than the increase in revenue from higher P, hence revenue rises.
• For example, let's assume that Q only falls to 20 (instead of 15) when P is increased to $350.

Price Elasticity 2

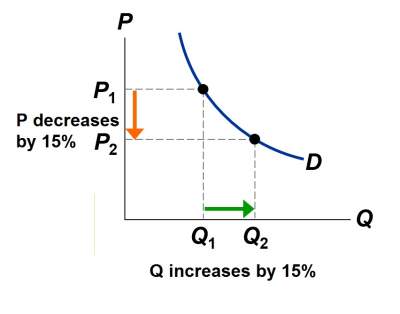
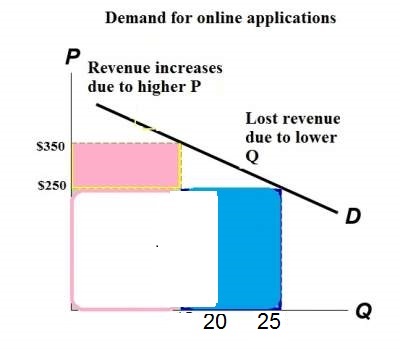
Elastic demand. In this case, elasticity = 0.67 If P = $250, Q = 25 and revenue = $5000 If P = $350, Q = 20 and revenue = $7000 When D is inelastic, a price increase causes revenue to rise.

Exercises