The Production Function

Introduction

A production function reveals the relationship between the quantity of inputs used to produce a good and the quantity of output of that good.
This function can be represented by an equation, graph, or table.

Example

Farmer Adam grows rice in his farm. He has 2 acres of land and can hire as many workers as he needs.
Adam's production funtion is shown as follows:

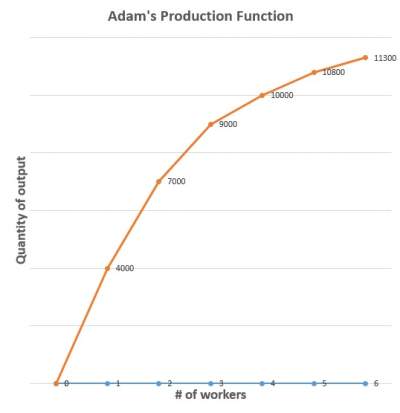
L (# of workers)	Q (Kilograms of rice)
0	0
1	4000
2	7000
3	9000
4	10000
5	10800
6	11300

Marginal Product

If Adam hires one more worker, his output will increase by the marginal product of labor.
The marginal product of any input is the increase in output arising from an additional unit of that input, holding all other inputs constant.
Notation:
ΔQ = change in output, ΔL = change in labor, and Marginal product of labor (MPL) = ΔQ / ΔL

Example

L (# of workers)	Q (Kilograms of rice)	ΔL	ΔQ	MPL
0	0
1	4000
		1	4000	4000
2	7000
		1	3000	3000
3	9000
		1	2000	2000
4	10000
		1	1000	1000
5	10800
		1	800	800
6	11300
		1	500	500

Why MPL?

Let's assume that Adam would like to hire an additional worker. What are the pros and cons?

The costs will increase by the salary given to the worker
the output will also increase by MPL, and this helps the business owner to make the right decision

The Reasons Behind MPL Drops Off

Farmer Adam's output rises by a smaller and smaller amount for each additional worker. Why?
Whenever Adam hires workers, the average worker has less land to work with and will be less productive.
So, MPL drops off as L rises whether the fixed input is land or capital including equipment and machines.
The marginal product of an input drops off as the quantity of the input increases (other things equal)

Example of Adam's Costs

Farmer Adam must pay $2000 per month for the land, no matter how much rice he grows.
The salary for a farm worker is about $3000 per month.
So farmer Adam's costs are related to how much rice he produces.

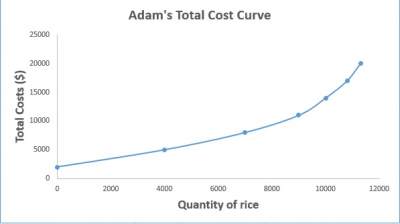
L (# of workers)	Q (Kilograms of rice)	Cost of Land	Cost of Labor	Total Costs
0	0	$2000	$0	$2000
1	4000	$2000	$3000	$5000
2	7000	$2000	$6000	$8000
3	9000	$2000	$9000	$11000
4	10000-	$2000	$12000	$14000
5	10800	$2000	$15000	$17000
6	11300	$2000	$18000	$20000

Q (Kilograms of rice)	Total Cost
0	2000
4000	5000
7000	8000
9000	11000
10000	14000
10800	17000
11300	20000

Marginal Cost

Marginal Cost (MC) is the increase in Total Cost from producing an additional unit. The formula is: MC = ΔTC / ΔQ

Example

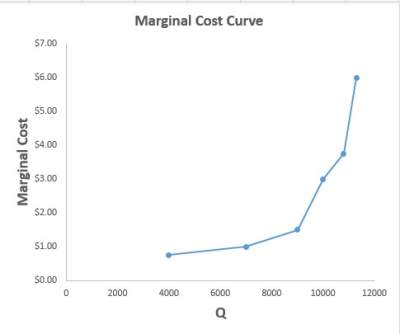
Q (Kilograms of rice)	Total Cost	ΔQ	ΔTC	Marginal Cost (MC)
0	$2000
4000	$5000
		4000	$3000	$0.75
7000	$8000
		3000	$3000	$1.00
9000	$11000
		2000	$3000	$1.50
10000	$14000
		1000	$3000	$3.00
10800	$17000
		800	$3000	$3.75
11300	$20000
		500	$3000	$6.00

Q (Kilograms of rice)	Total Cost	Marginal Cost
0	2000
4000	5000	$0.75
7000	8000	$1.00
9000	11000	$1.50
10000	14000	$3.00
10800	17000	$3.75
11300	20000	$6.00

Why MC?

Let's assume that Adam is rational and wants to maximize his profit.
To increase profit, does he need to produce more or less rice?
Here, Adam needs to think at the margin using the MC.
If MC is less than the revenue he would get from selling it, then Adam's profits rise if he produces more.

For more details, please contact me here.
Date of last modification: 2019