Topics covered here are as follows:
- Logic
- Existential Quantifier
- Precedence of Quatifiers
Logic
Definitions:
Logic is the study of the principles and methods that distinguish between a valid and an invalid argument.
Statement is a declarative sentence that is either true (T) or false (F) but not both. A statement is also referred to as a proposition.
Examples:
- 3+4 = 7.
- It is Friday today.
If a proposition is true, we say that it has a truth value of "True". If a proposition is false, its truth value is "falseQuot.
The truth values "true" and "false" are, respectively, denoted by the letters T and F.
Examples:
- "4 + 3 = 7" and "Sevilla is a city in Spain"
- "The grass is green" or " It is sunny today"
- "Computer Science is not difficult to me"
AND, OR, NOT are called Logical Connectives.
Symbolic Representation
Statements are symbolically represented by letters such as P, p, q, r, s, T, . . .
Examples:
- P = "Rome is the capital of Italy".
- q ="20 is divisible by 3".
The table below shows the details of logic connectivity
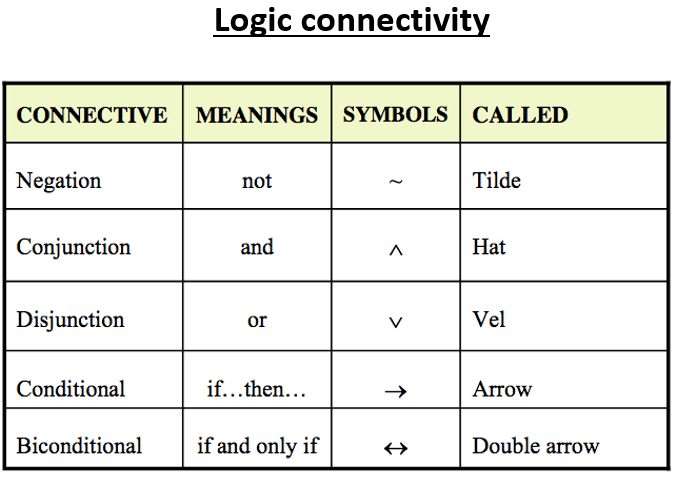
Examples
- p= "Cairo is the capital of Egypt".
- q="16 is divisible by 3".
- P ∧ q =" Cairo is the capital of Egypt and 16 is divisible by 3".
- P ∨q="Cairo is the capital of Egypt or 16 is divisible by 3".
- ~P = "It is not the case that Cairo is the capital of Egypt" or simply "Cairo is not the capital of Egypt".
Truth Table
Truth table specifies the truth value of a compound proposition for all possible truth values of its constituent propositions.
Negation(~)
If p is a statement variable, then negation of p,"not p", is denoted as "~p".
It has opposite truth value from p i.e., if p is true, then ~p is false; if p is false, then ~p is true.
Truth Table for ~p
| p | ~p |
| T | F |
| F | T |
Conjunction (∧)
Assume p and q are statements and the conjunction of p and q is "p and q", denoted as "p ∧q".
Note the following regarding the conjunction
- p∧q is true when both p and q are true.
- p∧q is false when either p or q is false, or both are false.
The Truth Table for p∧q is illustrated below:
Truth Table for p∧q
| p | q | p∧q |
| T | T | T |
| T | F | F |
| F | T | F |
| F | F | F |
Disjunction (∨) or Inclusive OR
Assume p and q are statements and the disjunction of p and q is "p or q", denoted as "p ∨q".
Note the following regarding the disjunction
- p∨q is true when either p or q is true, or both are true.
- p∨q is false when both p and q are false.
The Truth Table for p∨q is illustrated below:
Truth Table for p∨q
| p | q | p∨q |
| T | T | T |
| T | F | T |
| F | T | T |
| F | F | F |
Exclusive OR
When OR is used in its exclusive sense, the statement "p or q" mean "p or q but not both" or "p or q but not p and q"
which translates into symbols as (p∨q) ∧ ~(p∧q). It is abbreviated as p⊕q or p XOR q.
The Truth Table for p XOR q is illustrated below:
Truth Table for p⊕q
| p | q | p⊕q |
| T | T | F |
| T | F | T |
| F | T | T |
| F | F | F |
Conditional Statements
Consider the following statement: "If you get an A in Computer Science, then I will buy you your favorite phone."
This statement is composed of two simpler statements:
p:"You will get an A in Computer Science"
q:"I will buy you your favorite phone."
The original statement is then saying:
if p is true, then q is true, or simply, if p, then q.
This can also be expressed as: p implies q. It is denoted by p → q.
p → q. is false when p is true and q is false; otherwise it is true.
In p → q., the statement p is called the hypothesis (or antecedent) and q is called the conlcusion (or consequent)
The Truth Table for p → q is illustrated below:
Truth Table for p → q
| p | q | p→q |
| T | T | T |
| T | F | F |
| F | T | T |
| F | F | T |
Biconditional
Assume p and q are statement variables, the biconditional of p and q is "p if and only if q".
it is denoted p ↔ q. "if and only if" is abbreviated as iff.
The symbol (double headed arrwo) "↔" is the biconditional operator.
Note the following regarding the biconditional
- p↔q is true when both p and q are true.
- p↔q is false when either p or q is false.
The Truth table for p ↔ q is illustrated below.
Truth Table for p↔q
| p | q | p↔q |
| T | T | T |
| T | F | F |
| F | T | F |
| F | F | T |
Logic and Bit Operations
Computer bit operations correspond to the logical connectives.
By replacing true by a one and false by a zero in the truth tables for the operators ∧, ∨, and ⊕,
the tables shown for the corresponding bit operations are obtained.
Throughout this lesson and in various programming languages, the following notations will be used: AND, OR, and XOR for the operators ∧, ∨, and ⊕.
Truth Value of Bit
| Truth Value | Bit |
| T | 1 |
| F | 0 |
The table for the bit operators is shown below:
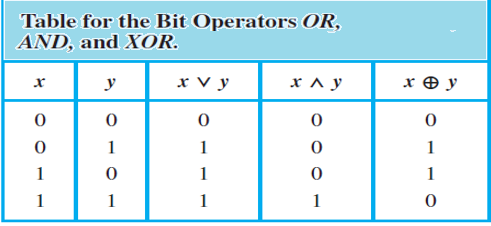
Practice Exercise and Solution
Exercise 1:
Find the bitwise AND, bitwise OR, and bitwise XOR of the bit strings 01 1011 0110 and 11 0001 1101.
Please note that in this lesson, bit strings will be split into blocks of four bits to make them easier to read.
Solution:
The bitwise AND, bitwise OR, and bitwise XOR of these strings are obtained by taking the AND, OR, and XOR of the corresponding bits:
- Bitwise AND: 01 0001 0100
- Bitwise OR: 11 1011 1111
- Bitwise XOR: 10 1010 1011
Logical equivalency
Definition:
If two logical expressions have the same logical values in the truth table, then these two expressions are logically equivalent.
For example, ~(~p) ≡ p and the Truth table is as under:
Truth Table for ~(~p)
| p | ~q | ~(~p) |
| T | F | T |
| F | T | F |
Practice Exercise and Solution
Exercise 2:
Show (prove) that ~(p∧q) and ~p &8743 ~q are not logically equivalent
Solution:
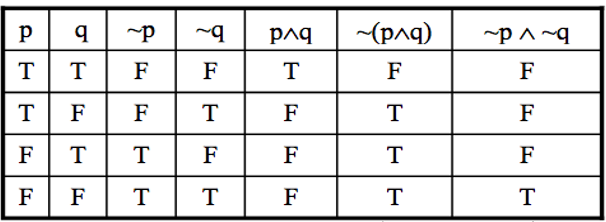
Exercise 3:
Find the truth table for the below:
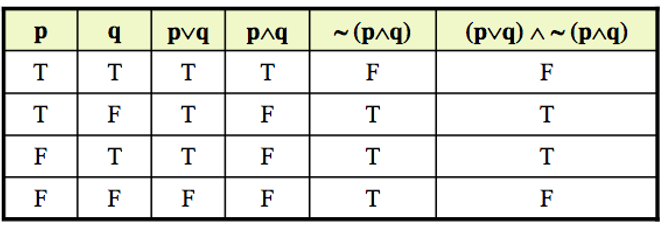
- ~p ∧ q
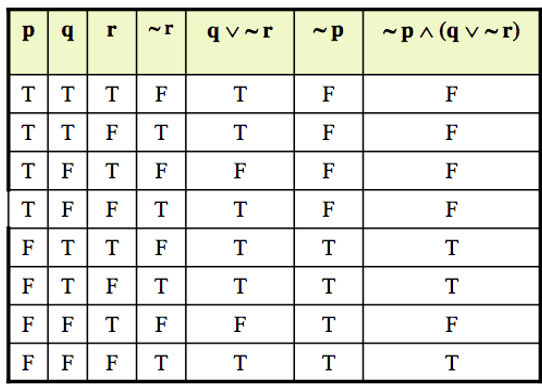
- ~p ∧ (q ∨ ~r)
- (p∨q) ∧ *#126(p∧q)
solutions:
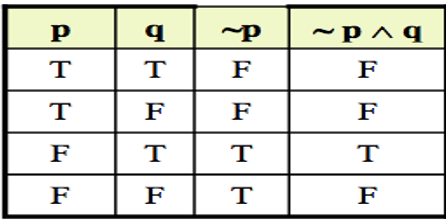
Tautology
A tautology is a statement form that is always true regardless of the truth values of the statement variables. A tautology is represented by the symbol “t”.
Example: The statement q ∨ ~q is a tautology and q ∨ ~q ≡ t. The truth table of this statement is as follows:
Truth Table for q ∨ ~q
| q | ~q | q ∨ ~q |
| T | F | T |
| F | T | T |
Contradiction
A contradiction is a statement form that is always false regardless of the truth values of the statement variables. A contradiction is represented by the symbol "c".
So if we have to prove that a given statement form is contradiction, we need to show the truth table for the statement form and if in the column of the given statement form all the entries are F, then we say that statement form is contradiction.
Let us see the following example: The statement form q ∧ ~ q is a contradiction.
Truth Table for q ∧ ~ q
| q | ~q | q ∧ ~ q |
| T | F | F |
| F | T | F |
Based on the last column, all the entries are F, hence it is a contradiction and it is noted as q ∧ ~ q ≡ c
Remarks
- Most statements are neither tautologies nor contradictions.
- The negation of a tautology is a contradiction and vice versa.
- In common usage we sometimes say that two statements are contradictory and their conjunction is a contradiction: they cannot both be true.
Logical Equivalence Invloving Tautology
Example: Show that r ∧ t ≡ r
Truth Table for r ∧ t
| r | t | r ∧ t |
| T | T | T |
| F | T | F |
Exercises
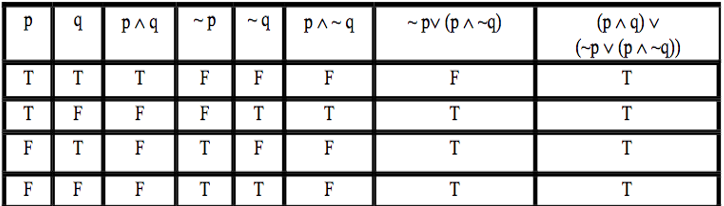
Exercise 4: Tautology
Use truth table to show that ( p ∧q ) ∨(~ p ∨( p ∧~q )) is a tautology.
Solution:
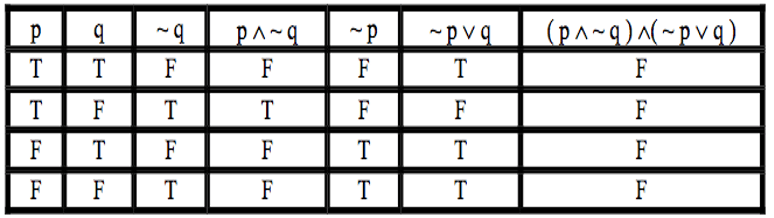
Exercise 5: Contradiction
Use truth table to show that (p ∧ ~q) ∧ (~p ∨q) is a contradiction.
Solution:
Translation from English to Synbols
Let r = "It is cold", and s = "It is sunny"
| Sentence | Symbolic Form |
| It is not cold. | ~r |
| It is cold and sunny. | r ∧ s |
| It is cold or sunny. | r ∨ s |
| It is not cold but sunny. | ~r ∧ s |
| It is neither cold nor sunny. | ~r ∧ ~s |
Exercises and Solutions
Exercise 6:
Let p, q and r be the following propositions:
- p = "you get an A on the final exam"
- q = "you do every exercise in this textbook"
- r = "you get an A in this class"
Question: Write the following propositions using p, q, and r and logical connectives.
- To get an A in this class it is necessary for you to get an A on the final exam. Solution: p → r
- You do exery in this textbook; You get an A on the final exam, implies, you get an A in this class. Solution: q ∧ p → r
- Getting an A on the final exam and doing every evercise in this textbook is sufficient for getting an A in this class. Solution: p ∧ q → r
Exercise 7:
Let p, q and r be the following propositions:
- p = "you have the flu"
- q = "you miss the final exam"
- r = "you pass the course"
Question: Express the following propositions as an English sentence.
- p → q. Solution: If you have flu, then you will miss the final exam.
- ~q → r. Solution: If you don’t miss the final exam, you will pass the course.
- ~p ∧ ~q → r. Solution: If you neither have flu nor miss the final exam, then you will pass the course.
Application of Logic
NOT-Gate
A NOT-gate (or inverter) is a circuit with one input and one output signal. If the input signal is 1, the output signal is 0. Conversely, if the input signal is 0, then the output signal is 1.
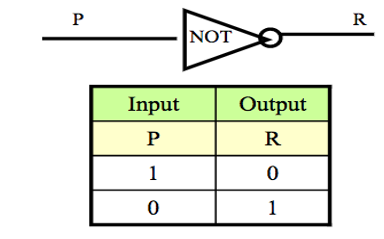
AND-Gate
An AND-gate is a circuit with two input signals and one output signal. If both input signals are 1, the output signal is 1. Otherwise the output signal is 0. Symbolic representation & Input/Output Table is shown below.
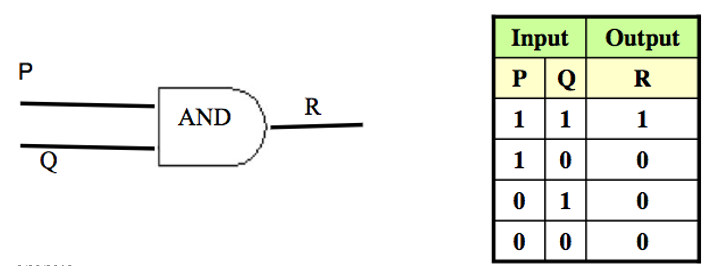
OR-Gate
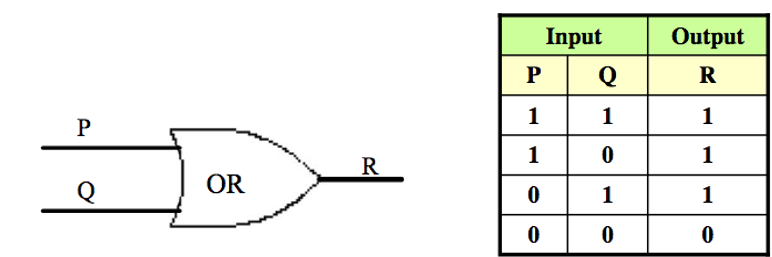
An OR-gate is a circuit with two input signals and one output signal. If both input signals are 0, then the output signal is 0. Otherwise, the output signal is 1.
Symbolic representation & Input/Output Table is shown below.
Combinatorial Circuit:
A Combinational Circuit is a compound circuit consisting of the basic logic gates such as NOT, AND, OR.
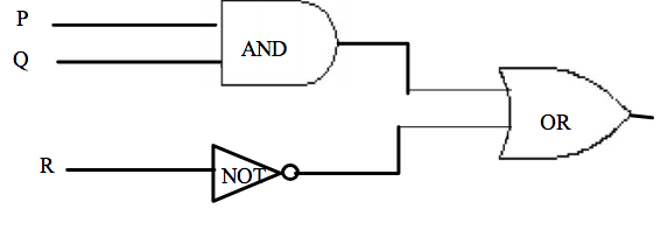
Exercise and Solution
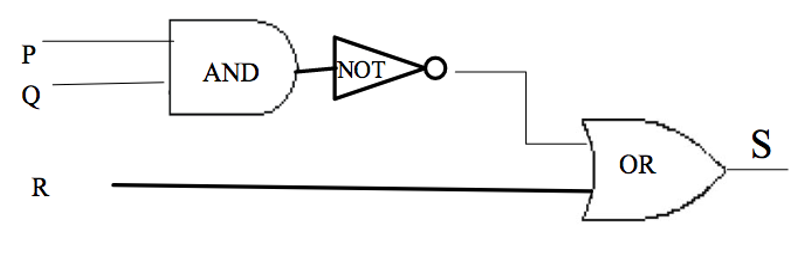
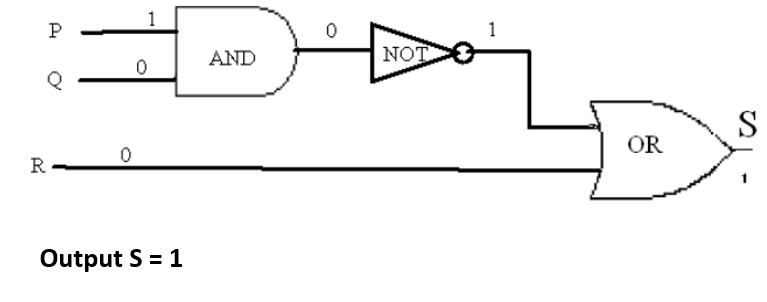
Determine the output for a given input:
Indicate the output of the circuit below when the input signals are P = 1, Q = 0 and R = 0. See the diagram below:
Solution:
For more details, please contact me here.
Date of last modification: 2024













