Introduction to Logical Equivalency and Triple bar logic
Definition:
If two logical expressions have the same logical values in the truth table, then these two expressions are logically equivalent.
For example, ~(~p) ≡ p and the Truth table is as under:
Truth Table for ~(~p)
| p |
~q |
~(~p) |
| T |
F |
T |
| F |
T |
F |
Practice Exercise and Solution
Exercise 2:
Show (prove) that ~(p ∧ q) and ~p ∧ ~q are n logically equivalent
Solution:
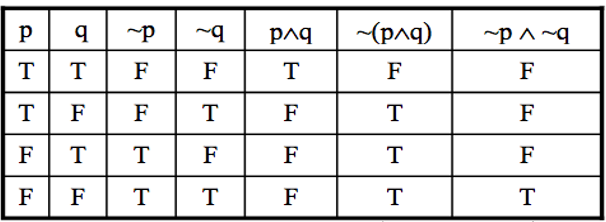
Exercise 3:
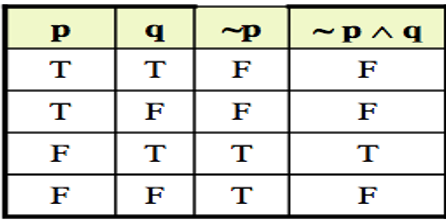
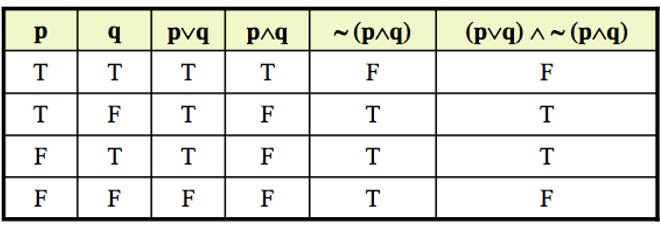
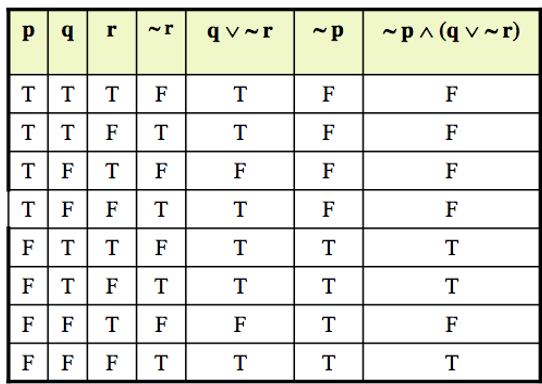
Find the truth table for the below:
- ~p ∧ q
- ~p ∧ (q ∨ ~r)
- (p∨q) ∧ ~(p∧q)
Solutions:
Tautology
A tautology is a statement form that is always true regardless of the truth values of the statement variables.
A tautology is represented by the symbol "t".
Example: The statement q ∨ ~q is a tautology and q ∨ ~q ≡ t. The truth table of this statement is as follows:
Truth Table for q ∨ ~q
| q |
~q |
q ∨ ~q |
| T |
F |
T |
| F |
T |
T |
Contradiction
A contradiction is a statement form that is always false regardless of the truth values of the statement variables. A contradiction is represented by the symbol "c".
So if we have to prove that a given statement form is contradiction, we need to show the truth table for the statement form and if in the column of the given statement form all the entries are F, then we say that statement form is contradiction.
Let us see the following example: The statement form q ∧ ~ q is a contradiction.
Truth Table for q ∧ ~ q
| q |
~q |
q ∧ ~ q |
| T |
F |
F |
| F |
T |
F |
Based on the last column, all the entries are F, hence it is a contradiction and it is noted as q ∧ ~ q ≡ c
Remarks
- Most statements are neither tautologies nor contradictions.
- The negation of a tautology is a contradiction and vice versa.
- In common usage we sometimes say that two statements are contradictory and their conjunction is a contradiction: they cannot both be true.
For more details, please contact me here.



