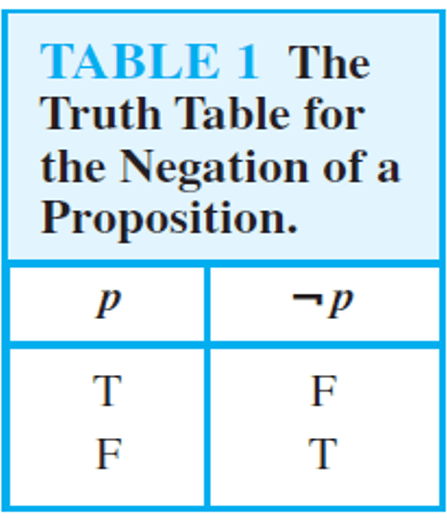
Truth Tables
A truth table displays the relationships between truth values (T or F) of different propositions.
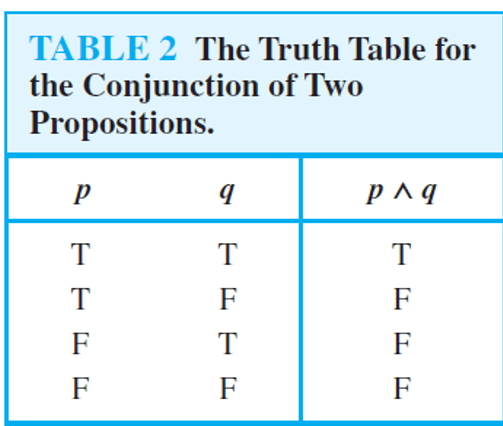
Conjunction
Let p and q be propositions. The proposition ″p and q″ denoted by p∧q, is true when both p and q are true and is false otherwise. The proposition p∧q is called the conjunction of p and q.
Assume the following:
p = ″Omar has obtained very high overall score in the SAT Exam″
q = ″ The subject Biology in Omar's SAT results was the highest score″
Hence, p∧q = ″Omar has obtained very high score in the SAT Exam, and the subject Biology in Omar's SAT results was the highest score″
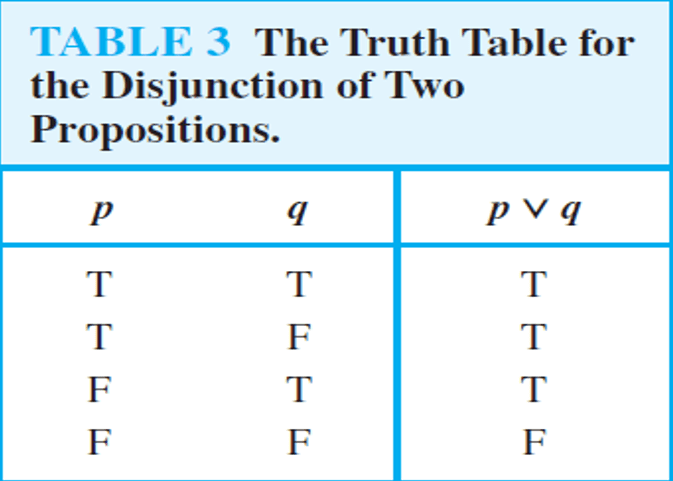
Disjunction
Let p and q be propositions. The proposition ″p or q″ denoted by p∨q, is false when both p and q are false and is true otherwise.
The proposition p∨q is called the disjunction of p and q.
Assume the following:
p∨q (the or is used inclusively, i.e., p∨q is true when either p or q or both are true).
p = ″Omar has obtained very high overall score in the SAT Exam″
q = ″ The subject Biology in Omar's SAT results was the highest score″
Hence, p∨q = ″Omar has obtained very high score in the SAT Exam, or the subject Biology in Omar's SAT results was the highest score″
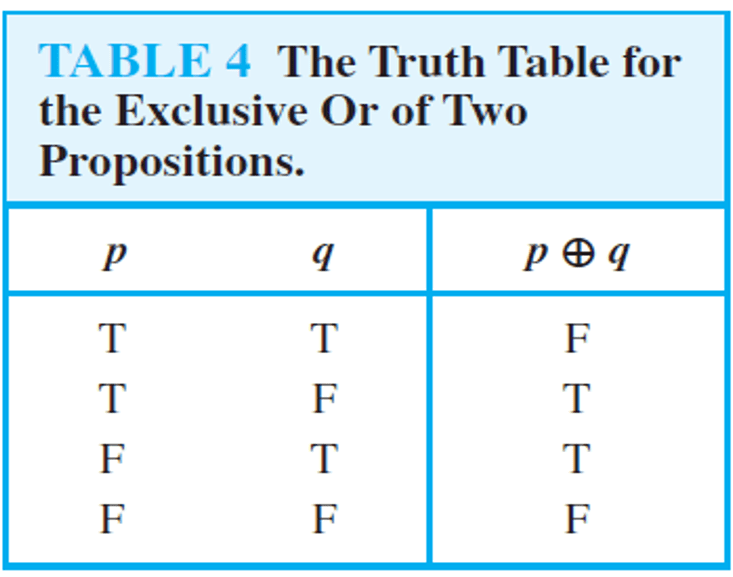
Exclusive or
Let p and q be propositions. The proposition "p exclusive or q" denoted by p⊕q, is true when exactly one of p and q is true and it is false otherwise.
″Students who have taken calculus or computer science, but not both, can enroll in this class.″
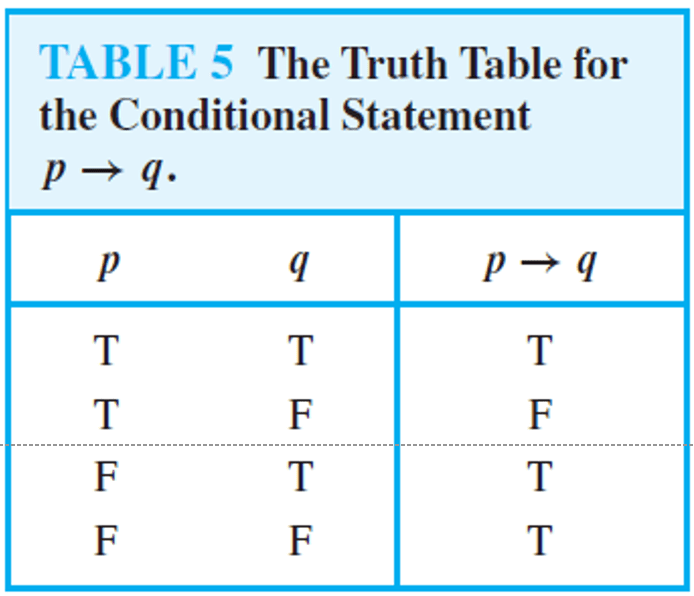
Conditional Statement (implication)
Let p and q be propositions. The conditional statement p → q is the proposition ″if p, then q.″
The conditional statement p→q is false when p is true and q is false, and true otherwise.
In the conditional statement p→q, p is called the hypothesis and q is called the conclusion.
A conditional statement is also called implication.
Example: ″If you get 100% on the final, then you will get an A.″
- You get 100%, you get an A. Answer: True
- You get 100%, you do not get A. Answer: False
- You do not get 100%, you get an A. Answer: True
- You do not get 100%, you do not get an A. Answer: True
Another example
- If Adam got an A in Computer Science, then 4 + 5 = 9
is true from the definition of a conditional statement, because its conclusion is true.
- If Adam got an A in Biology, then 6 + 7 = 9
is true if Adam did not get an A in Biology, even though 6+7=9 is false.
Biconditional
Example: p = "You can take the flight,"
q = "You buy a ticket. "
Then p↔q is the statement "You can take the flight if and only if you buy a ticket."
Try these examples below and check if it is true or false:
- if you buy a ticket and can take the flight. Answer: True
- if you do not buy a ticket and you cannot take the flight. Answer: True
- you do not buy a ticket, but you can take the flight. Answer: False
- you buy a ticket but you cannot take the flight. Answer: False
Truth Tables of Compound Propositions
Four important logical connectives including conjunctions, disjunctions, conditional statements, and biconditional statements,
as well as negations can be used to build up compound propositions.
Example:
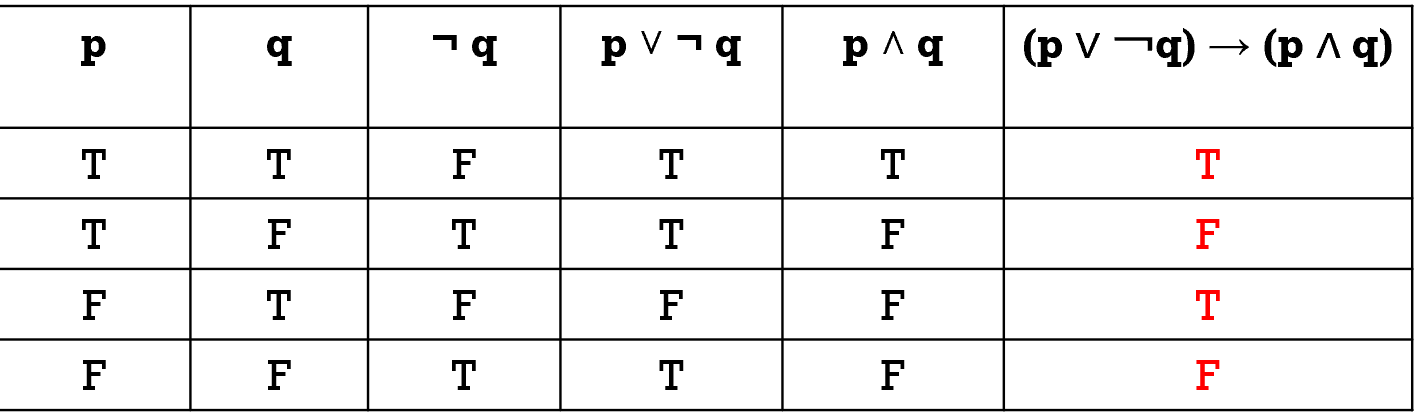
Construct the truth table of the compound proposition (p ∨ ¬q) → (p∧q)
For two propositional variables p and q, there are four rows in this truth table,
one for each of the pairs of truth values TT, TF, FT, and FF.
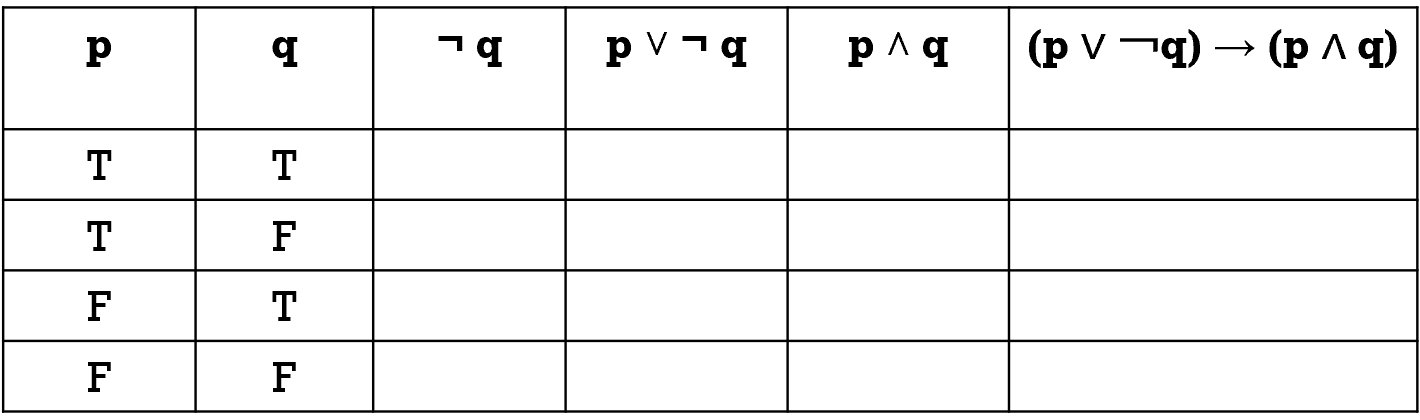
Try to fill out the above table:
The completed table is as below:
Precedence of Logical Operators
We will generally use parentheses to specify the order in which logical operators in a compound proposition are to be applied.
Otherwise, logical operators are applied in the following precedence.

Logic and Bit Operations
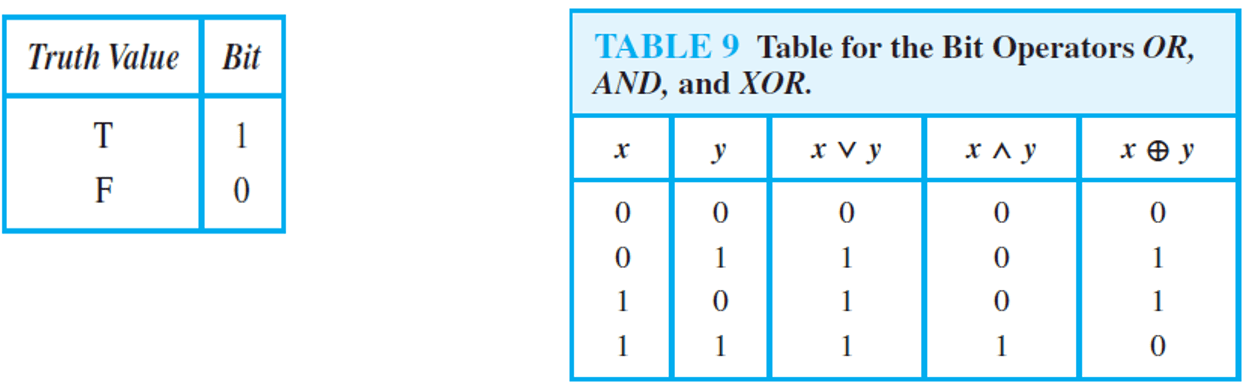
We need to encode two values True and False:
Computers represents data and programs using 0s and 1s
Logical truth values: True and False
A bit is sufficient to represent two possible values:
0 (False) or 1(True)
A variable that takes on values 0 or 1 is called a Boolean variable.
Definition: A bit string is a sequence of zero or more bits.
The length of this string is the number of bits in the string.
Example: Find the bitwise OR, bitwise AND, and bitwise XOR of the bit strings 01 1011 0110 and 11 0001 1101.
01 1011 0110
11 0001 1101
11 1011 1111 bitwise OR
01 0001 0100 bitwise AND
10 1010 1011 bitwise XOR
For more details, please contact me here.
Date of last modification: 2021








