Logic
Definitions:
Logic is the study of the principles and methods that distinguish between a valid and an invalid argument.
Statement is a declarative sentence that is either true (T) or false (F) but not both. A statement is also referred to as a proposition.
Examples:
- 3+4 = 7.
- It is Friday today.
If a proposition is true, we say that it has a truth value of "True". If a proposition is false, its truth value is "falseQuot.
The truth values "true" and "false" are, respectively, denoted by the letters T and F.
Examples:
- "4 + 3 = 7" and "Sevilla is a city in Spain"
- "The grass is green" or " It is sunny today"
- "Computer Science is not difficult to me"
AND, OR, NOT are called Logical Connectives.
Symbolic Representation
Statements are symbolically represented by letters such as P, p, q, r, s, T, . . .
Examples:
- P = "Rome is the capital of Italy".
- q ="20 is divisible by 3".
The table below shows the details of logic connectivity
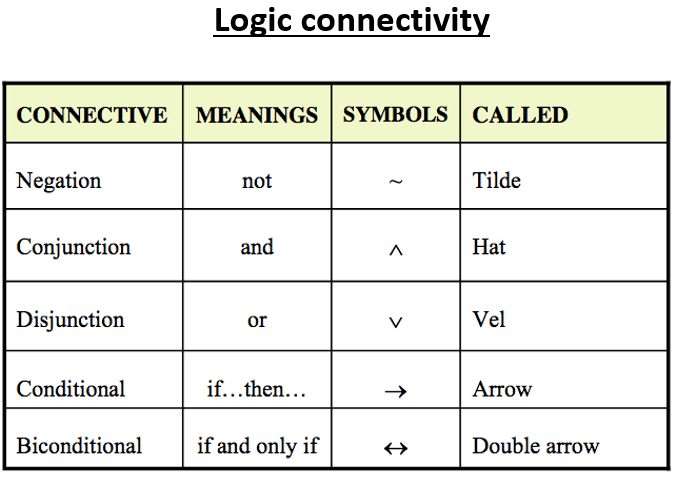
Examples
- p= "Cairo is the capital of Egypt".
- q="16 is divisible by 3".
- P ∧ q =" Cairo is the capital of Egypt and 16 is divisible by 3".
- P ∨q="Cairo is the capital of Egypt or 16 is divisible by 3".
- ~P = "It is not the case that Cairo is the capital of Egypt" or simply "Cairo is not the capital of Egypt".
For more details, please contact me here.
Date of last modification: 2024
