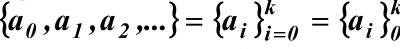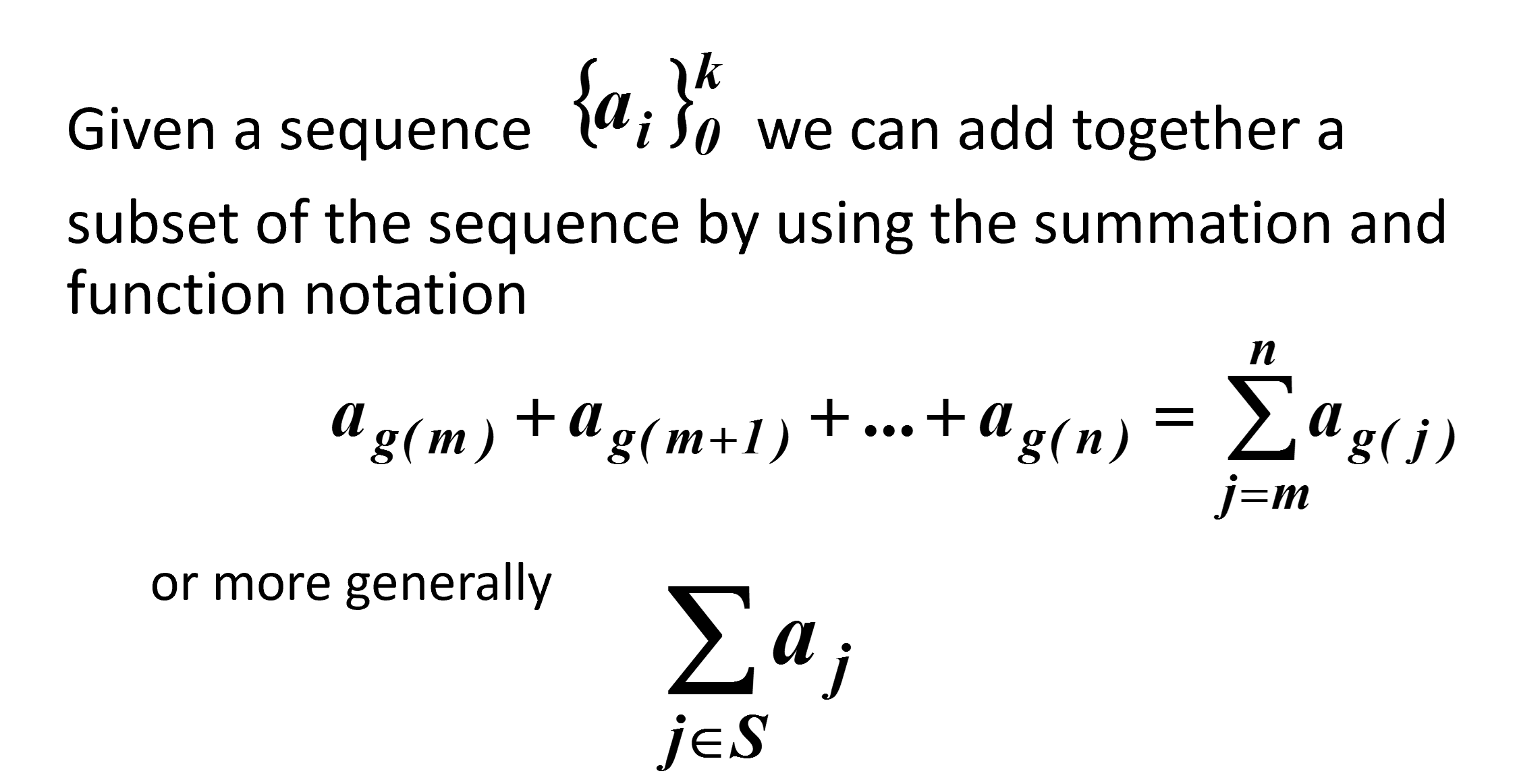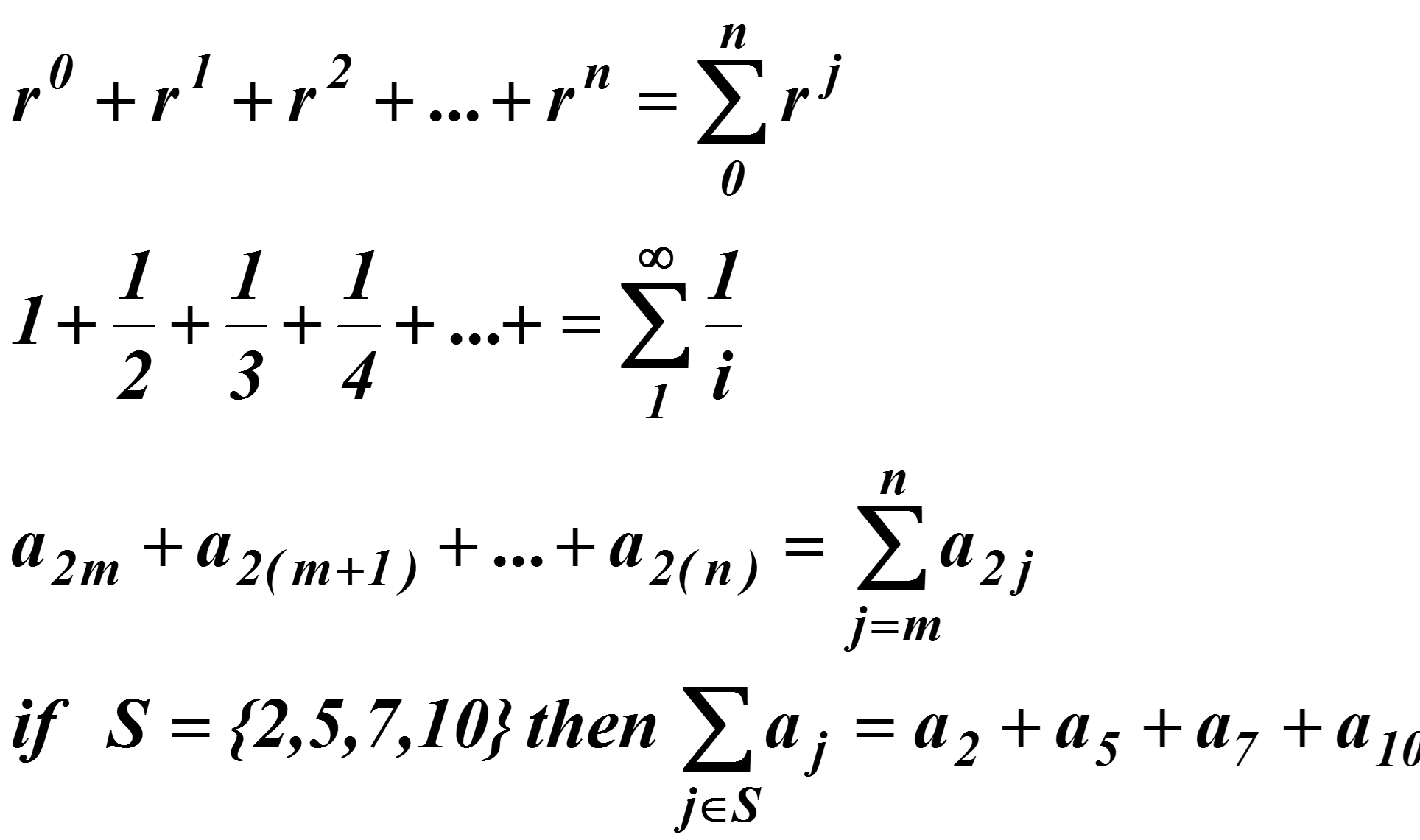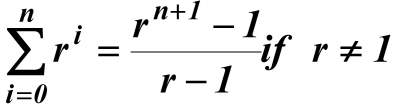Functions: Surjective, Bijective, Injective
Definition:
A function ffrom a set P to a set Q is an assignment of exactly one element of Q to each element of P.
We write f(p) = q
if q is the unique element of Q assigned by the function f to the element p of P.
If f is a function from P to Q, we write
f: P→Q
Here is what we say about this function:
- If f: P→Q, we say that P is the domain of f and Q is the codomain of f.
- If f(p) q, we say that q is the image of p and p is the pre-image of q.
- The range of f: P→Qis the set of all images of elements of P.
- We say that f: P→Q maps P to Q.
Example
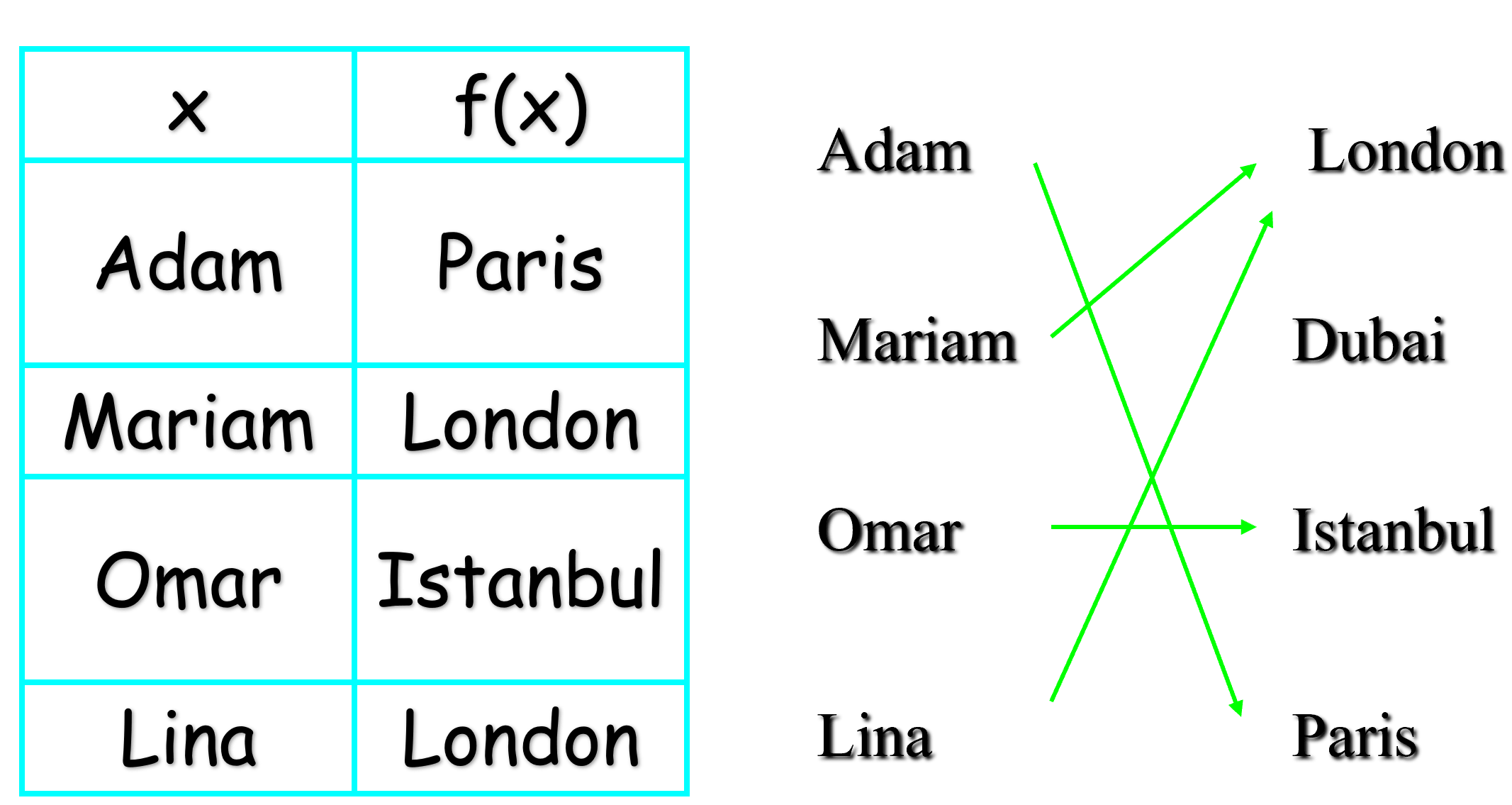
Assume the following function f: P→Q with
P = {Adam, Mariam, Omar, Lina}
Q = {London, Dubai, Istanbul, Paris}
f(Adam) = Paris
f(Mariam) = London
f(Omar) = Istanbul)
f(Lina) = Dubai
Here is the range of f is Q.
If we make the following changes:
f(Adam) = Dubai then f is still a function but the range is {Dubai, London, Istanbul}
Another way to represent f:
Injections, Surjections and Bijections
A function f: P→Q is said to be one-to-one (or injective), if and only if
∀x, y∈P (f(x) = f(y) → x=y)
Basically, f is one-to-one if and only if it does not map two distinct elements of P onto the same element of Q.
Example
Is f one-to-one?
f(Adam) = Dubai
f(Mariam) = London
f(Omar) = Istanbul)
f(Lina) = Dubai
The answer is no because Adam and Lina are mapped onto the same element of the image.
Properties of Functions
- A function f: P→Q is called onto, or surjective, if and only if for every element q∈Q there is an element p∈P with f(p) = q.
-
In other words, f is onto if and only if its range is its entire codomain.
-
A function f: P→Q is a one-to-one correspondence, or a bijection, if and only if it is both one-to-one and onto.
-
Obviously, if f is a bijection and P and Q are finite sets, then ▕P▏=▕Q▏
Examples
See the below function and check if it is injective, surjective, or bjiective.

Answer: f is neither.
Question: What if Omar is also connected to Dubai?
Answer: Here, f is not even a function.
Question: What if Lina is also connected to Dubai?
Answer: In that case, f is injective, surjective, as well as bijective.
Composition
Let f: O→P , g: Q→O. The composition of f with g, denoted f∘g, is the function from Q to P defined by
f∘g(x) = f(g(x))
Example
let f(x) = x2 and g(x)=x ‒ 3 are functions from R to R
Find the compositions f∘g and g∘f
Answer
f∘g(x) = f(g(x)) = f(x ‒ 3) = (x ‒ 3)2
g∘f(x) = g(f(x)) = g(x2) = x2 ‒ 3
Which means that f∘g and g∘f are generally different.
Sequences and Summations
Definition:A sequence is a function from a subset of the natural numbers (usually of the form {0, 1, 2, . . . } to a set S.
Note: the sets {0, 1, 2, 3, . . . , k} and {1, 2, 3, 4, . . . , k}
are called initial segments of N.
Notation: if f is a function from {0, 1, 2, . . .} to S we usually denote f(i) by ai and we write.
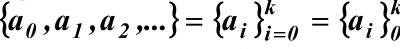
where k is the upper limit (usually ∞).
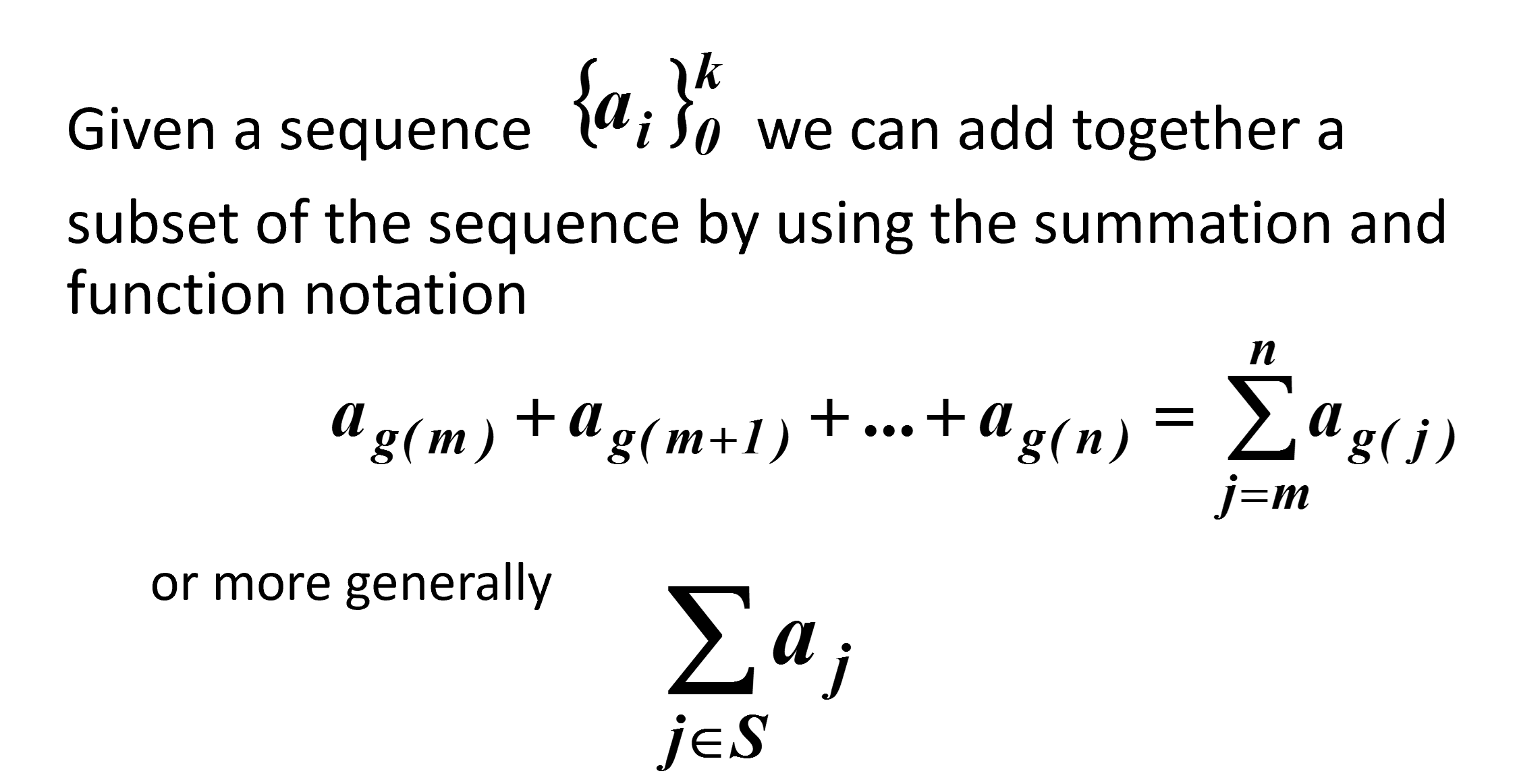
Example
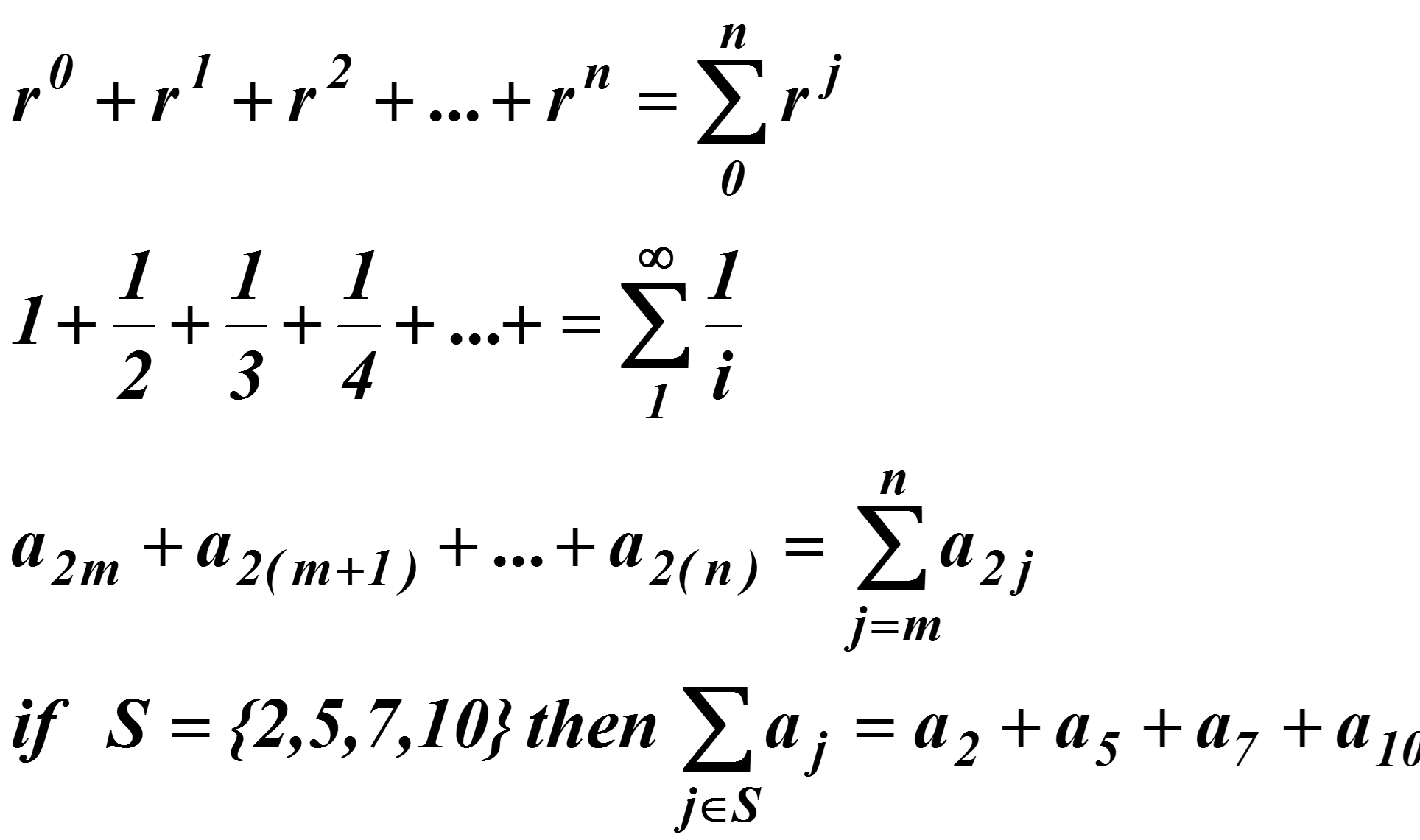
Geometric Progression
A geometric progression is a sequence of the form a, ar, ar2, ar3, ar4, . . . .
Try to prove that
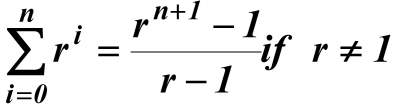
(Try to figure out what it is if r = 1).
You should also be able to determine the sum
- if the index starts at k vs. 0
- if the index ends at something other than n (e.g., n– 1, n+1, etc.).
For more details, please contact me here.
Date of last modification: February 20, 2019