Kinetic Molecular Theory
Introduction
This theory was developed to explain the gas behavior, hence called the "theory of moving molecules".
Assumptions:
- Gases consist of a large number ofmolecules in constant random motion.
- Volume of individual molecules isnegligible compared to volume of container.
- Intermolecular forces (forces between gas molecules) negligible.
- Energy can be transferred between molecules, but total kinetic energy is constant at constant temperature.
- Average kinetic energy of molecules is proportional to temperature.
The theory of moving molecules helps us understand the following:
- Pressure and temperature at the molecular level
- Pressure of a gas results from the number of collisions per unit time on the walls of container.
- Magnitude of pressure is given by how often and how hard the molecules strike.
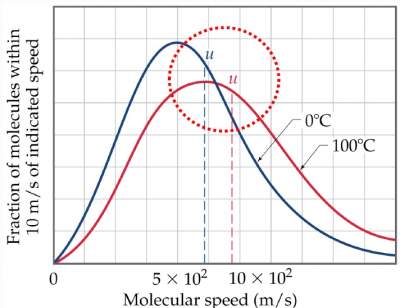
- The average kinetic energy of the gas molecules increases as the temperature increases.
Application to Gas Laws
- As volume increases at constant temperature, the average kinetic of the gas (u) remains constant.
However, as volume increases, gas molecules will have to travel further to hit the walls of the container.
Therefore, pressure decreases.
- If temperature increases at constant volume, the average kinetic energy of the gas molecules (u) increases.
Therefore, there are more collisions with the container walls and the pressure increases.
The average kinetic energy (ε) is related to the root mean square speed (u) via the relation:
ε = ½mu2
Hence, as u increases, (ε) will also increase
Remark:
The average kinetic energy (ε) depends on the mass of the molecules (m) and their speed (u)
Where the speed (u) is related to the molar mass of the gas molecule and the temperature through the relation:
u =
√ 3RT/M
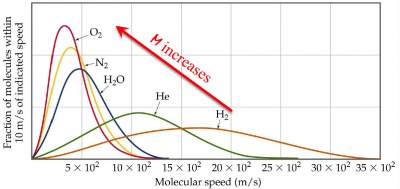
Therefore, the speed of a gas molecule increases with temperature and decreases with its molar mass:
Exercises on Kinetic Molecular Theory
Exercise on Finding the RMS Speed of He atom
Check your answers here:
Solution to the Exercise on Finding the RMS Speed of He atom
For more details, please contact me here.
Date of last modification: 2024


