Examples
An economist uses as a model for the demand of a product:
Qd = − 2p + 300
where Qd is the quantity demanded, in units and p is the price of one unit, in dollars.
The model used for the supply of the same product is: Qs = 4p − 120
where Qs is the quantity supplied, in units and p is the price of one unit, in dollars.
Questions
(1) Draw an accurate graph of both of these equations for p = 30 to p = 150.
Use the horizontal axis for p and the vertical axis for Qd and Qs.
Draw both graphs on the same diagram.
Tables for graphing the equations are as follows:
Demand: Qd = − 2p + 300
Supply: Qs = 4p − 120
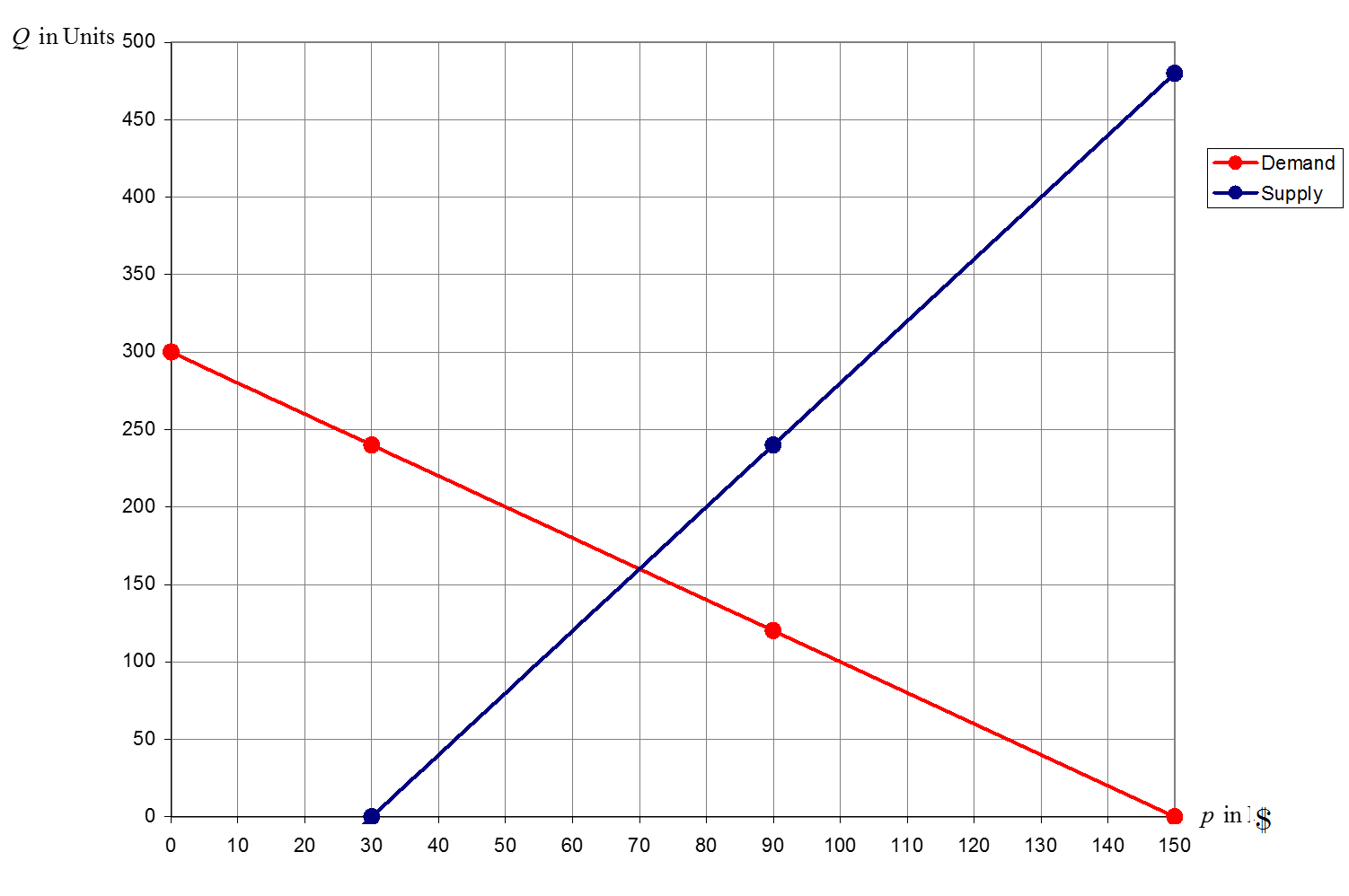
The graph of these two equations is as follows:
Question 2
Economists call the price where quantity supplied is equal to quantity demanded the "equilibrium price."
Use your graph to find the equilibrium price.
The equilibrium price is the value of p at the point where the graphs intersect.
If the graphs are drawn accurately on graph paper it is possible to read the equilibrium price accurately.
Equilibrium price = $70
Notice that the slope of the demand is negative, and the slope of the supply is positive.
- For p &th $70, demand exceeds supply.
- For p > $70, supply exceeds demand.
| p | Qd | Qs | Shortage (−) or excess (+) |
| 50 | 200 | 80 | − 120 |
| 60 | 180 | 120 | − 60 |
| 70 | 160 | 160 | 0 |
| 80 | 140 | 200 | +60 |
| 90 | 120 | 240 | +120 |
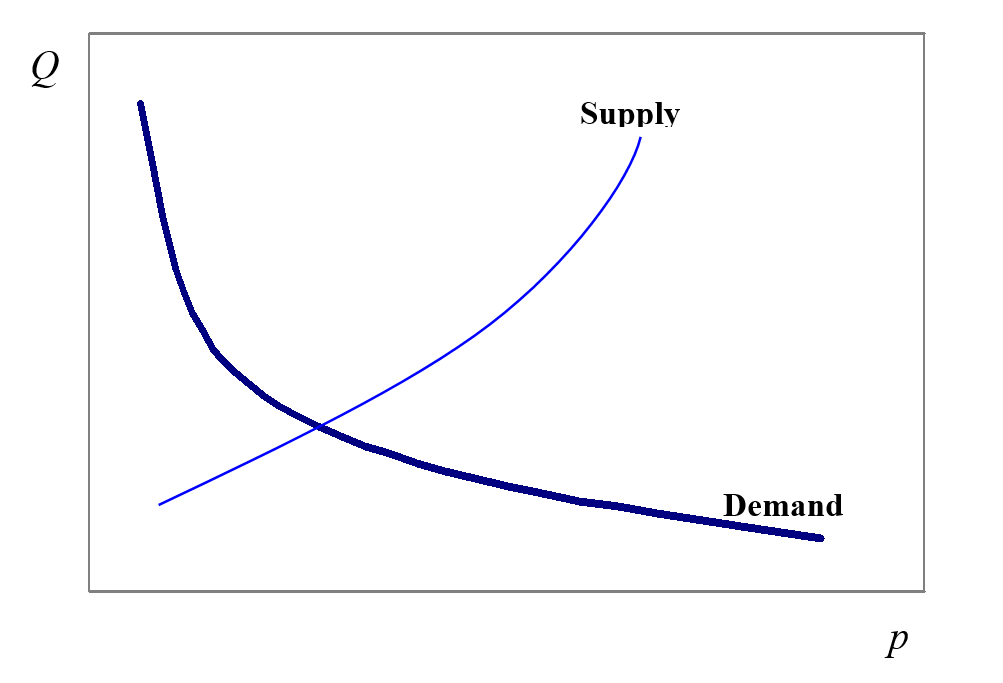
Although economists use linear models for supply and demand, these might not always be appropriate.
The graph above shows the demand to be 300 units when the price is zero.
In real life, the demand might be infinitely large if the price was really zero.
So for very small values of the price, a non-linear model might be more appropriate.
A more realistic model for demand and supply might, when graphed, look as follows:
A graph like this would have a more complicated mathematical form than a linear equation.
Please access the following link to do an exercise about supply and demand:
Supply and Demand
Please access the following link to see the solution of the supply and demand exercise using Excel :
Excel Solution of the the Supply and Demand exercise
Please access the following link to do an extra exercise about supply and demand:
Supply and Demand: Exercise with solution
For more details, please contact me here.
Date of last modification: March 19, 2019