Introduction to Statistics

Introduction

Statistics is a branch of mathematics, which involves:

Collecting data
Organizing and analyzing data
Drawing conclusions from data

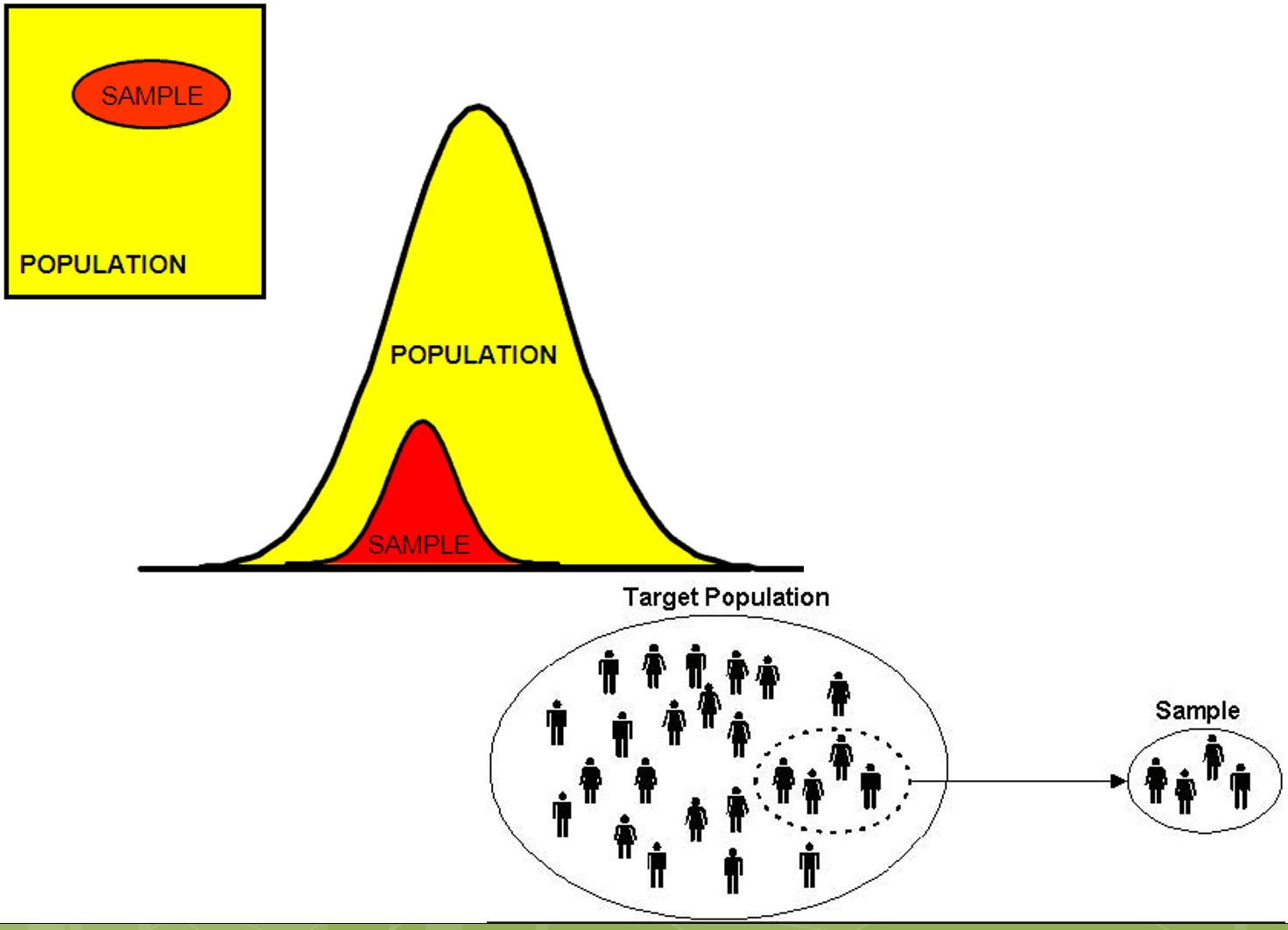
Population vs. Sample

Population: The entire group of objects or individuals whose properties are to be analyzed. The population always contains all elements of the group that we would like to analyze.
Sample: A part or subset of the population used to gain information about the whole. See illustration below:
population vs sample

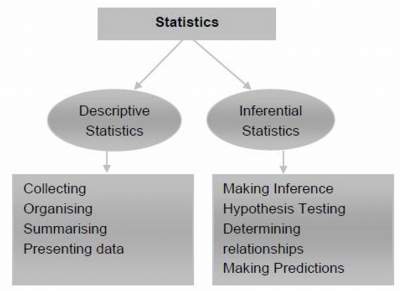
Descriptive and Inferential Statistics

Descriptive statistics is the science of:

collecting data,
classifying data, and
summarizing data. In this course we shall learn some of the basic concepts of descriptive statistics.

If a researcher gathers data from a sample and uses the resulting statistics to reach conclusions about the parameters of the population from which the sample was taken, the statistics are inferential statistics. See illustration below about two categories of statistics:
About Statistics

Classification of Data

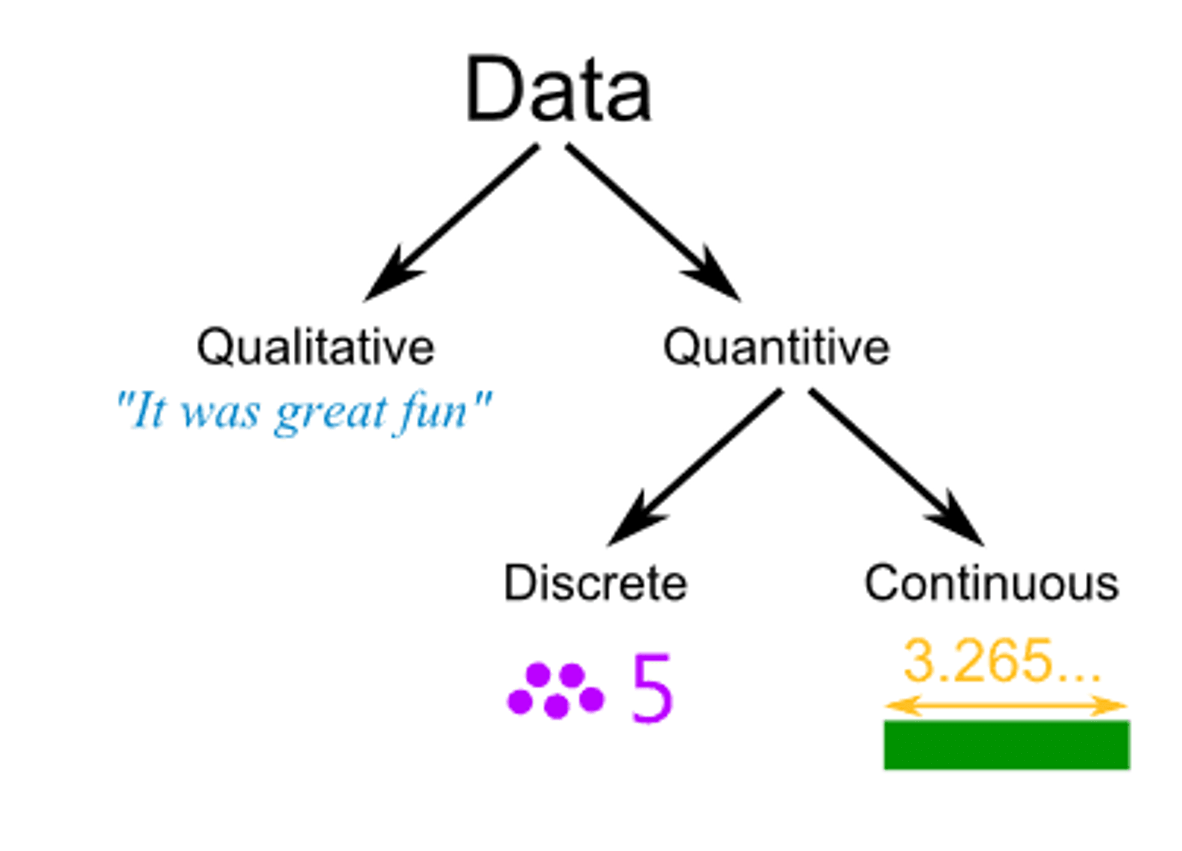
Data can be classified into two broad types: qualitative and quantitative.
Qualitative date:
Example: Gender, occupation, nationality, and color They are not measured with a scale; they represent categories only.

Quantitative date:
Example: Ages, height, weight, speed, number of patients in a hospital. Numerical data can be manipulated by arithmetic expressions such as addtion and substration.

Variables

Variables may be discrete or continuous.
A discrete variable is a variable that can take only selected values.
Examples:

The number of students in a class. There cannot be 20 and half students in the class, but there can be 20 or 21 students.
The number of rooms in a house.
A discrete variable is mostly the result of a count.

A continuous variable is one that can assume any value within a specified interval.
Examples:

Height of a student in the class.
the time required to complete a task
weight of a shipment
the profits or revenues of a company
The height of a student cannot jump from 1.7 m to 1.8 meters
It must assume every value between 1.5 m and 1.6 m at some time

A continuous variable is mostly the result of a measurement.
About data

Now, it is time to answer simple questions then check your answers with the provided solutions.

For more details, please contact me here.
Date of last modification: March 5, 2019